Similar Triangle Proofs Practice : Proofs And Triangle Congruence Theorems Practice Geometry Questions Dummies

There are many other proofs of the pythagorean theorem. 14.06.2016 · then the two triangles formed are similar to the original triangle and each other. Here is one of the oldest proofs that the square on the long side has the same area as the other squares. Thus, triangle ebf has sides with lengths ka, kb, and kc. Now use angles of a triangle add to 180° to find angle bac: Do that again but for a different diameter;

Angle bac + 55° + 90° = 180° angle bac = 35° finding a circle's center. Similar Triangles Proofs Two Column Proof Practice And Quiz Reasoning Activities Similar Triangles Math Teacher — Similar Triangles Proofs Two Column Proof Practice And Quiz Reasoning Activities Similar Triangles Math Teacher from i.pinimg.com

Draw a square along the hypotenuse (the longest side). Thanks to the triangle sum theorem, all we have to show is that two angles of one triangle are congruent to two angles of another triangle to show similar triangles. Also, since the opposite sides of a rectangle are congruent, b = ka + kc and c = a + kb. There are many other proofs of the pythagorean theorem. Angle bac + 55° + 90° = 180° angle bac = 35° finding a circle's center. Watch the animation, and pay attention when the triangles start sliding around.

Watch the animation, and pay attention when the triangles start sliding around.

Now use angles of a triangle add to 180° to find angle bac: 21.01.2020 · as we saw with the aa similarity postulate, it's not necessary for us to check every single angle and side in order to tell if two triangles are similar. Do that again but for a different diameter; Thus, triangle ebf has sides with lengths ka, kb, and kc. Also, since the opposite sides of a rectangle are congruent, b = ka + kc and c = a + kb. We can use this idea to find a circle's center: Full curriculum of exercises and videos. Draw a right angled triangle on the paper, leaving plenty of space. Where the diameters cross is the center. Watch the animation, and pay attention when the triangles start sliding around. Draw a square along the hypotenuse (the longest side). Draw a right angle from anywhere on the circle's circumference, then draw the diameter where the two legs hit the circle;

Here is one of the oldest proofs that the square on the long side has the same area as the other squares. Draw a right angle from anywhere on the circle's circumference, then draw the diameter where the two legs hit the circle; Since fb = fd, fd = kc.

Thus, triangle ebf has sides with lengths ka, kb, and kc. Completing Proofs Involving Congruent Triangles Using Sss Practice Geometry Practice Problems Study Com — Completing Proofs Involving Congruent Triangles Using Sss Practice Geometry Practice Problems Study Com from study.com

Draw a right angled triangle on the paper, leaving plenty of space. Angle bac + 55° + 90° = 180° angle bac = 35° finding a circle's center. Here is one of the oldest proofs that the square on the long side has the same area as the other squares. Where the diameters cross is the center. Since fb = fd, fd = kc. By the aa similarity theorem, triangle ebf is similar to triangle cab. We can use this idea to find a circle's center:

Draw a right angled triangle on the paper, leaving plenty of space.

Angle bac + 55° + 90° = 180° angle bac = 35° finding a circle's center. Draw a square along the hypotenuse (the longest side). Do that again but for a different diameter; We can use this idea to find a circle's center: Thanks to the triangle sum theorem, all we have to show is that two angles of one triangle are congruent to two angles of another triangle to show similar triangles. Also, since the opposite sides of a rectangle are congruent, b = ka + kc and c = a + kb. You may want to watch the animation a few times to understand … By the aa similarity theorem, triangle ebf is similar to triangle cab. Full curriculum of exercises and videos. There are many other proofs of the pythagorean theorem. 21.01.2020 · as we saw with the aa similarity postulate, it's not necessary for us to check every single angle and side in order to tell if two triangles are similar.

Here is one of the oldest proofs that the square on the long side has the same area as the other squares. Angle bac + 55° + 90° = 180° angle bac = 35° finding a circle's center. Now, let k be the similarity ratio between triangles ebf and cab.

Now, let k be the similarity ratio between triangles ebf and cab. Geometry Triangle Proof Vocabulary Practice Ppt Download — Geometry Triangle Proof Vocabulary Practice Ppt Download from slideplayer.com

Since fb = fd, fd = kc. By the aa similarity theorem, triangle ebf is similar to triangle cab. 14.06.2016 · then the two triangles formed are similar to the original triangle and each other. There are many other proofs of the pythagorean theorem. Here is one of the oldest proofs that the square on the long side has the same area as the other squares. Also, since the opposite sides of a rectangle are congruent, b = ka + kc and c = a + kb. Now, let k be the similarity ratio between triangles ebf and cab. Watch the animation, and pay attention when the triangles start sliding around. Draw a right angled triangle on the paper, leaving plenty of space. Now use angles of a triangle add to 180° to find angle bac:

We can use this idea to find a circle's center:

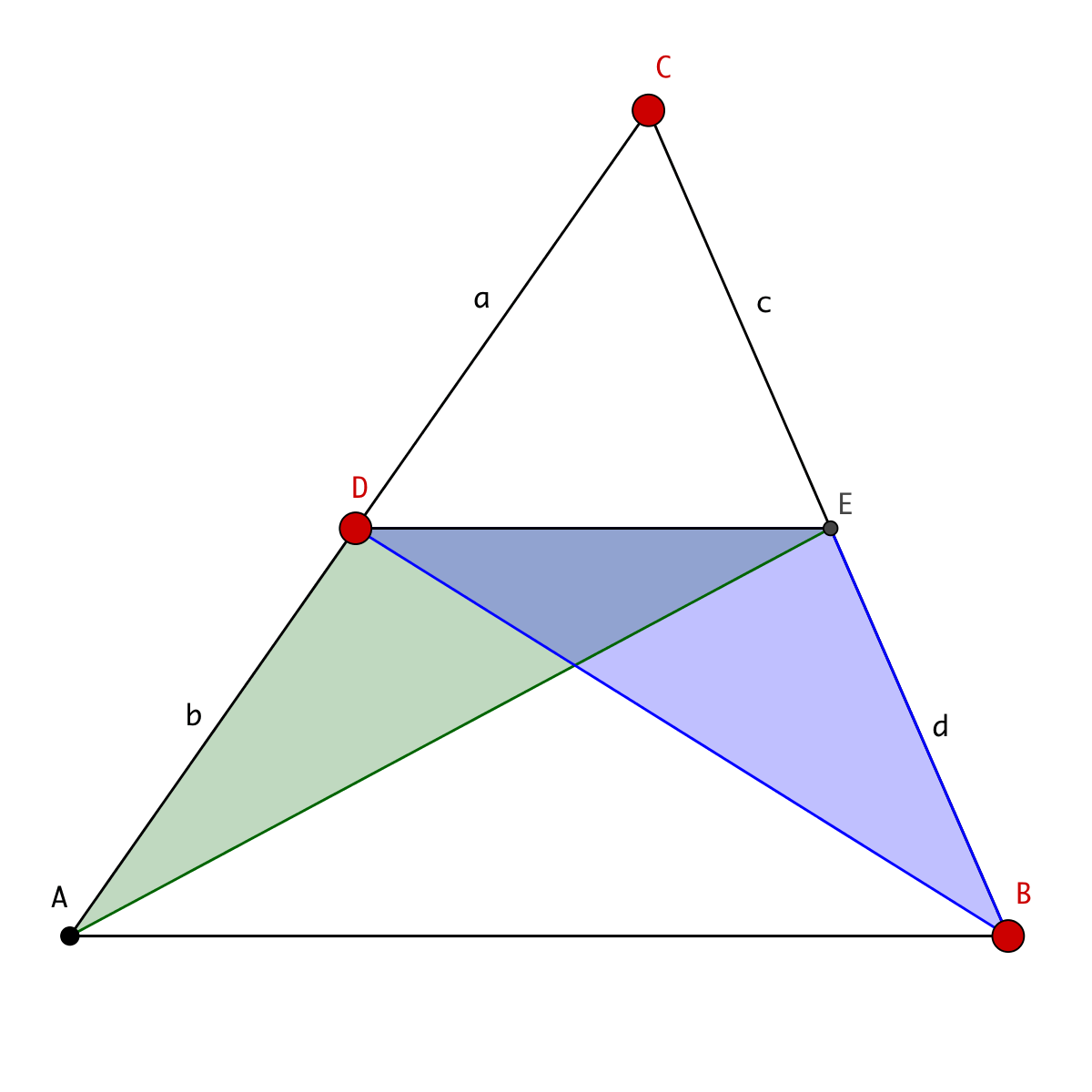
14.06.2016 · then the two triangles formed are similar to the original triangle and each other. Here is one of the oldest proofs that the square on the long side has the same area as the other squares. Draw a square along the hypotenuse (the longest side). Thanks to the triangle sum theorem, all we have to show is that two angles of one triangle are congruent to two angles of another triangle to show similar triangles. You may want to watch the animation a few times to understand … We can use this idea to find a circle's center: Angle bac + 55° + 90° = 180° angle bac = 35° finding a circle's center. Since fb = fd, fd = kc. Also, since the opposite sides of a rectangle are congruent, b = ka + kc and c = a + kb. By the aa similarity theorem, triangle ebf is similar to triangle cab. Thus, triangle ebf has sides with lengths ka, kb, and kc. Where the diameters cross is the center. There are many other proofs of the pythagorean theorem. Now, let k be the similarity ratio between triangles ebf and cab.

Similar Triangle Proofs Practice : Proofs And Triangle Congruence Theorems Practice Geometry Questions Dummies. Draw a right angled triangle on the paper, leaving plenty of space. Also, since the opposite sides of a rectangle are congruent, b = ka + kc and c = a + kb. Draw a square along the hypotenuse (the longest side). Thus, triangle ebf has sides with lengths ka, kb, and kc. Now, let k be the similarity ratio between triangles ebf and cab. Thanks to the triangle sum theorem, all we have to show is that two angles of one triangle are congruent to two angles of another triangle to show similar triangles.

Now, let k be the similarity ratio between triangles ebf and cab. Congruent Triangle Proof Practice Mathbitsnotebook Geo Ccss Math

Now use angles of a triangle add to 180° to find angle bac: Thanks to the triangle sum theorem, all we have to show is that two angles of one triangle are congruent to two angles of another triangle to show similar triangles. You may want to watch the animation a few times to understand … Full curriculum of exercises and videos.

21.01.2020 · as we saw with the aa similarity postulate, it's not necessary for us to check every single angle and side in order to tell if two triangles are similar. Area Of Similar Triangles Formula Theorem Proof Examples

Do that again but for a different diameter; Angle bac + 55° + 90° = 180° angle bac = 35° finding a circle's center. We can use this idea to find a circle's center: Since fb = fd, fd = kc. There are many other proofs of the pythagorean theorem.

By the aa similarity theorem, triangle ebf is similar to triangle cab. 2

Angle bac + 55° + 90° = 180° angle bac = 35° finding a circle's center. Watch the animation, and pay attention when the triangles start sliding around. Full curriculum of exercises and videos.

Also, since the opposite sides of a rectangle are congruent, b = ka + kc and c = a + kb. Triangle Proofs Common Core High School Geometry

Thus, triangle ebf has sides with lengths ka, kb, and kc. Since fb = fd, fd = kc.

Now use angles of a triangle add to 180° to find angle bac: Now, let k be the similarity ratio between triangles ebf and cab. Draw a right angle from anywhere on the circle's circumference, then draw the diameter where the two legs hit the circle; We can use this idea to find a circle's center:

Draw a square along the hypotenuse (the longest side). Area Of Similar Triangles Formula Theorem Proof Examples

Angle bac + 55° + 90° = 180° angle bac = 35° finding a circle's center.

Since fb = fd, fd = kc. Similar Triangles Proofs Teaching Resources Teachers Pay Teachers

Thanks to the triangle sum theorem, all we have to show is that two angles of one triangle are congruent to two angles of another triangle to show similar triangles. By the aa similarity theorem, triangle ebf is similar to triangle cab. Here is one of the oldest proofs that the square on the long side has the same area as the other squares.

Now use angles of a triangle add to 180° to find angle bac:

By the aa similarity theorem, triangle ebf is similar to triangle cab.

Where the diameters cross is the center. 7 Ideas For Teaching Congruent Triangles Mrs E Teaches Math

Draw a right angle from anywhere on the circle's circumference, then draw the diameter where the two legs hit the circle;

$Watch the animation, and pay attention when the triangles start sliding around. Geometry Similar Triangles$

21.01.2020 · as we saw with the aa similarity postulate, it's not necessary for us to check every single angle and side in order to tell if two triangles are similar.